在概率论与统计学中，期望与方差是两个重要的概念，它们能够帮助我们理解随机变量的特征和分布。期望是一个随机变量的平均值，而方差则衡量了随机变量偏离其期望值的程度。本文将深入探讨期望与方差公式的应用和推导过程，帮助读者更好地理解并运用这两个公式。

期望的含义与计算方法

1.期望的定义及意义：期望是对随机变量取值的加权平均，它能够反映随机变量的中心位置。

2.离散型随机变量的期望计算：根据定义，离散型随机变量的期望可以通过将每个取值与其对应的概率相乘，并求和得到。

3.连续型随机变量的期望计算：对于连续型随机变量，期望的计算需要使用积分来求解。

方差的含义与计算方法

4.方差的定义及意义：方差是随机变量与其期望之间的差异程度的平方的期望值。

5.离散型随机变量的方差计算：方差的计算可以通过将每个取值与其对应的概率相乘，并求和得到。

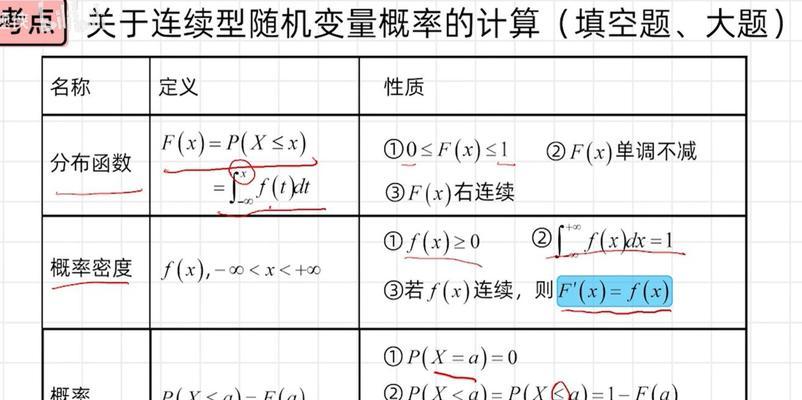
6.连续型随机变量的方差计算：对于连续型随机变量，方差的计算需要使用积分来求解。

期望与方差的应用案例

7.期望的应用案例：期望可以用于预测某一事件的平均结果，比如在赌博游戏中计算平均盈利。

8.方差的应用案例：方差可以衡量风险和不确定性，比如在金融领域中用于评估投资组合的稳定性。

期望与方差公式的推导

9.期望公式的推导过程：通过对离散型随机变量和连续型随机变量进行加权平均，推导出期望的公式。

10.方差公式的推导过程：通过对离散型随机变量和连续型随机变量偏离其期望值的差异进行平方和的加权平均，推导出方差的公式。

期望与方差公式的性质与扩展

11.期望的线性性质：期望具有线性性质，即对于常数和随机变量的线性组合，期望等于各个部分的加权平均。

12.方差的性质与扩展：方差具有一些特殊性质，比如方差的非负性和方差与线性变换的关系。

期望与方差公式的限制和局限性

13.期望与方差公式的局限性：期望与方差公式在某些情况下可能不适用，比如对于非线性变换和高阶矩的计算。

14.替代方法与改进：针对期望与方差公式的局限性，研究者们提出了一些替代方法和改进模型，用于更准确地描述随机变量的特征和分布。

15.与展望：期望与方差是概率论与统计学中基础而重要的概念，对于理解随机变量的特征和分布至关重要。通过对期望与方差公式的应用和推导的深入学习，我们能够更好地应用这些概念于实际问题中，同时也为进一步研究随机变量的其他特征和分布提供了基础。

本文对期望与方差公式的应用与推导进行了深入解析，介绍了期望和方差的含义及计算方法，并给出了应用案例。此外，文章还介绍了期望与方差公式的推导过程、性质与扩展、局限性以及替代方法与改进。期望与方差作为概率论与统计学中重要的概念，对于理解随机变量的特征和分布具有重要意义。通过本文的学习，读者能够更好地理解和运用期望与方差公式。